
3 X 5 Y 2 2 X Y 4 3y By Substitution Method Brainly In
Algebra Calculator is a calculator that gives stepbystep help on algebra problems See More Examples » x3=5 1/3 1/4 y=x^21 Disclaimer This calculator is not perfect Please use at your own risk, and please alert us if something isn't working Thank youAnswer (1 of 3) 2x3y=6 equation 1 2x3y=15 equation 2 substitute eq1 in eq2 then it comes 6 != 15 ie 6 is not equal to 15 hence x and y has no solution
3-(x-5)=y+2 2x+y)=4-3y by elimination method
3-(x-5)=y+2 2x+y)=4-3y by elimination method-So let's do that We're going to replace y with 5 plus x So this 9x plus 3y equals 15 becomes 9x plus 3 times y The second equation says y is 5 plus x So we're going to put 5 plus x there instead of a y 3 times 5 plus x is equal to 15 And now we can just solve for x We get 9x plus 3 times 5 is 15 plus 3 times x is 3x is equal to 15Then substitute the result for that variable in the other equation 3x2y=12,xy=5 3 x 2 y = 1 2, x y = 5 Choose one of the equations and solve it for x by isolating x on the left hand side of the equal sign Choose one of the equations and solve it for
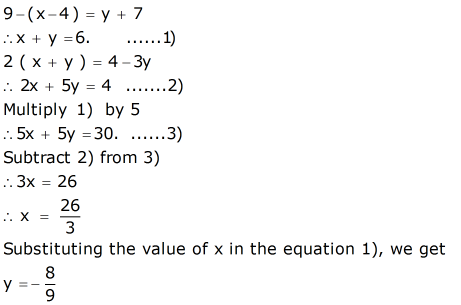
9 X 4 Y 7 2 X Y 4 3y Mathematics Topperlearning Com 5inhk66
Answer (1 of 2) The above ODE shows a linear equation which can be solved using Integration Factor Method xy' 3y =2x^5 Divide through by x (xy')/x (3/x)y =(2x^5)/x y' (3/x)y =2x⁴ IF=e^ln(3/x)=3/x Thus, IF=3/x IFy=∫2x⁴IF 3y/x =∫(2x⁴ 3)/x 3y/x =∫6x³ 3y/x=(6x⁴)/4 c Explanation by appling the laws of exponents ∙ x(am)n = a(m×n) ← (1) ∙ xam ×an = a(mn) (1) is extended to include all factors inside the parenthesis ⇒ (5x2y3)2 = 5(1×2) ×x(2×2) ×y(3×2) × × × × = 52 × x4 × y6 = 25x4y6 ⇒ (2x3y4)3 = 2(1×3) ×x(3×3) ×y(4×3) × × × × = 23 × x9 × y12 = 8x9y12Solve by matrix method 2x 3y 3z = 5 x 2y z = 4 3x y 2z = 3
Simple and best practice solution for 2(x4y)3(2x3y)= equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homeworkExample 6 Rewrite the expression x2y z5 with the last three terms enclosed in parentheses preceded by a minus sign x2yz5=x(2yz5) 23 Multiplication of Polynomials When multiplying monomials in which the variable x appears, we obtain products of the form x^(m)x^(n)The total number of factors of x in this product is m n, so that we have the following law of exponentsX2y=2x5,\xy=3 5x3y=7,\3x5y=23 x^2y=5,\x^2y^2=7 xyx4y=11,\xyx4y=4 3x^2=y,\x1=y xy=10,\2xy=1 systemofequationscalculator y = 3x 5, y = 2x 5 en
3-(x-5)=y+2 2x+y)=4-3y by elimination methodのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In | 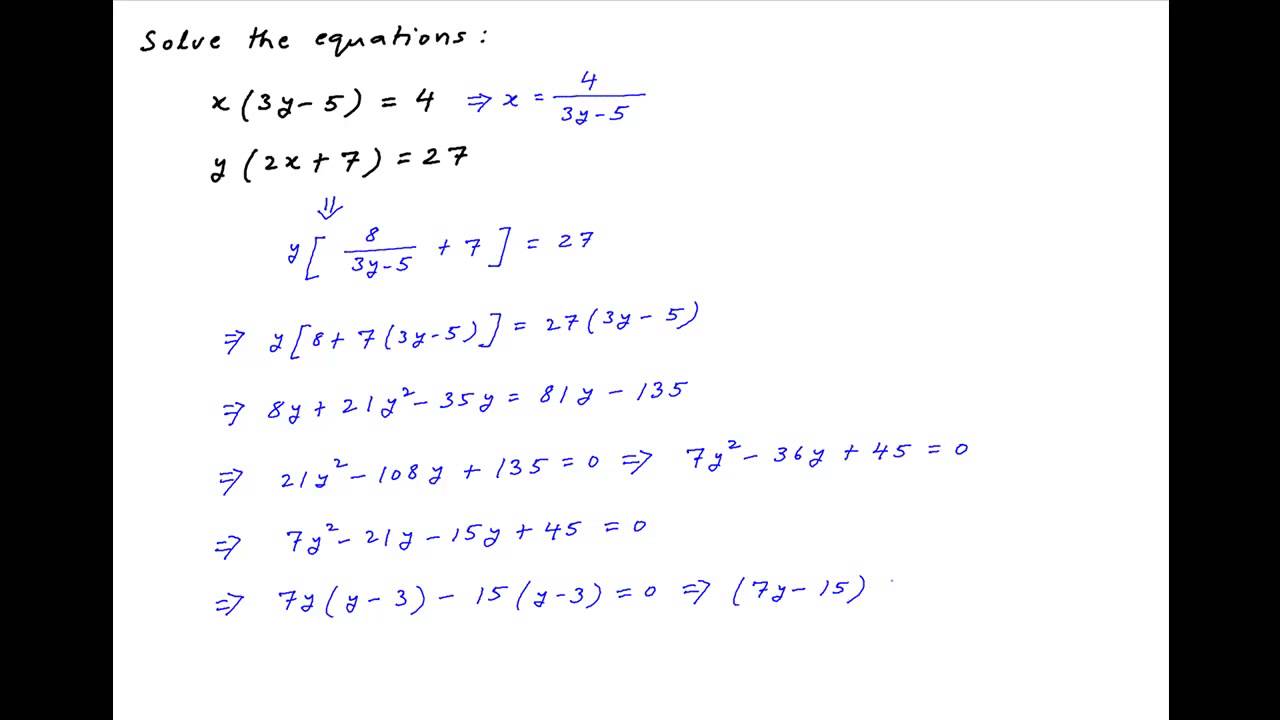 3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
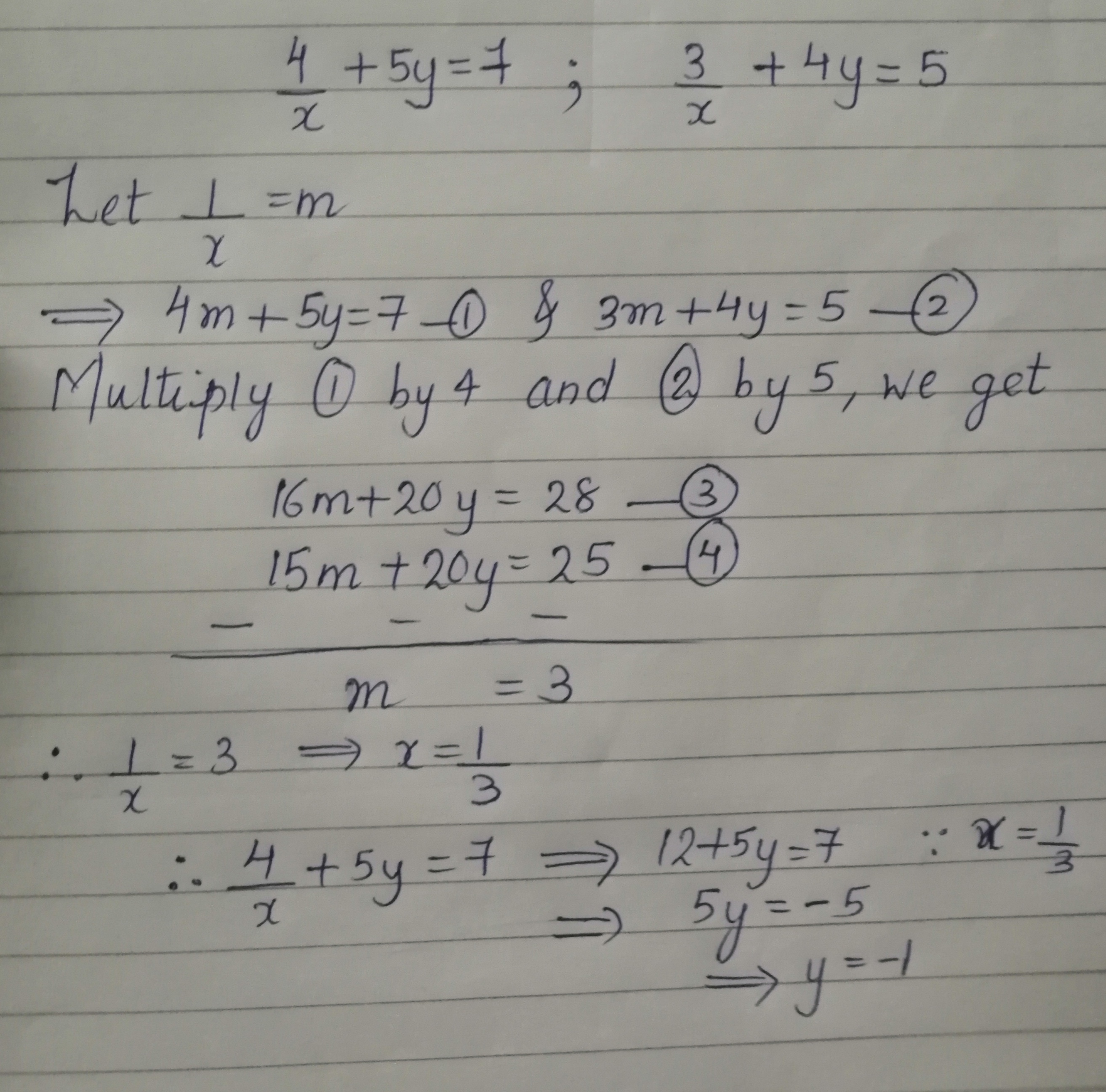 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
3 X 5 Y 2 2 X Y 4 3y Brainly In | 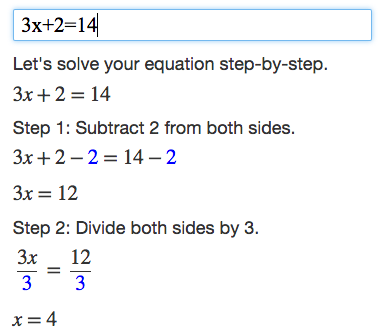 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In | 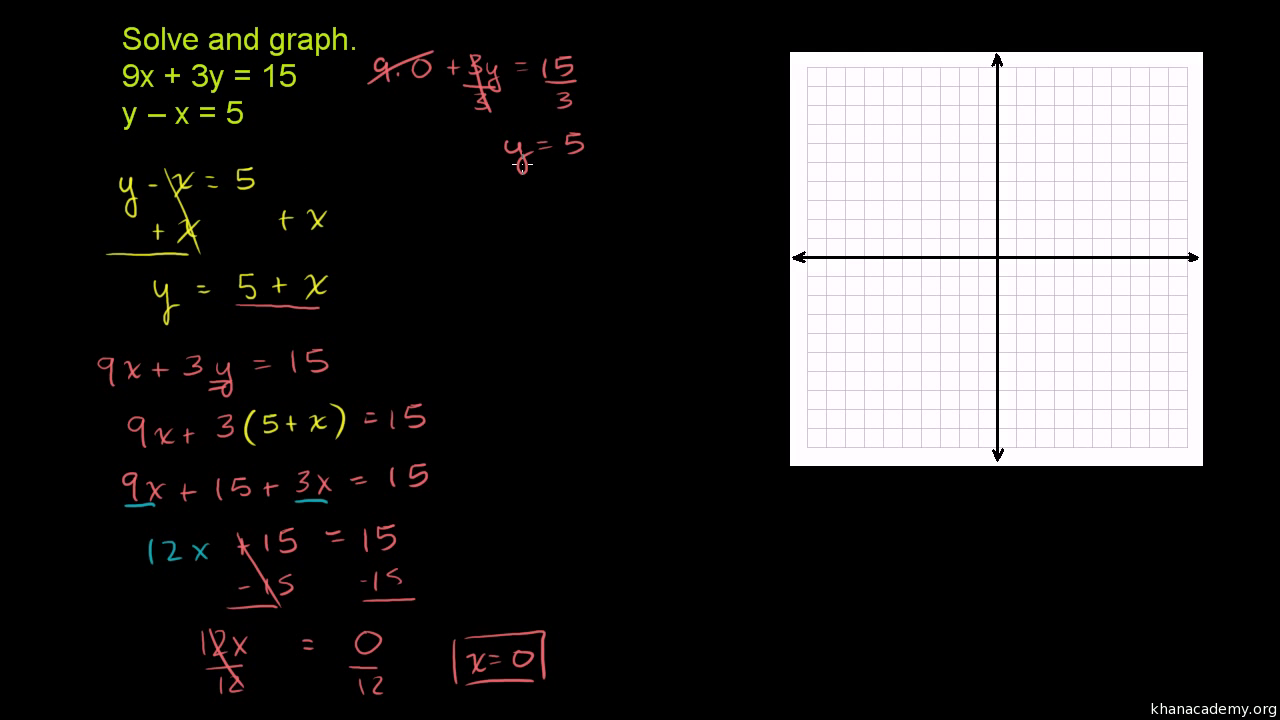 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 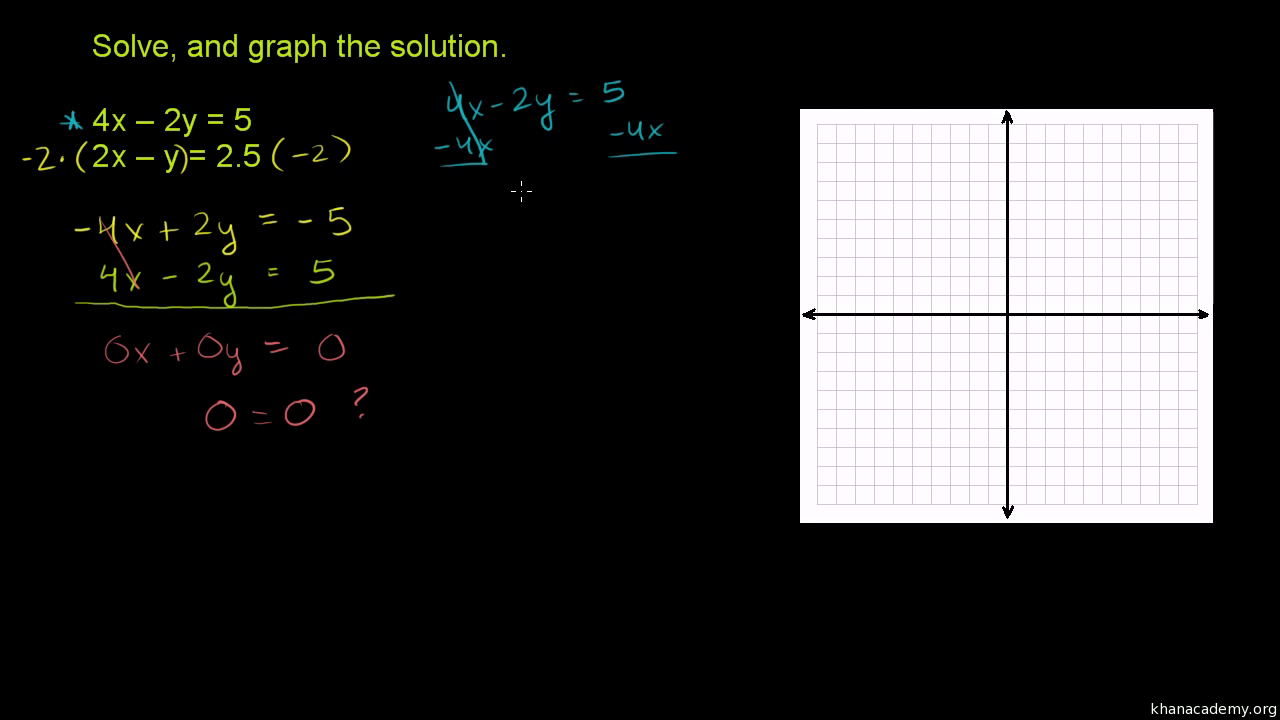 3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
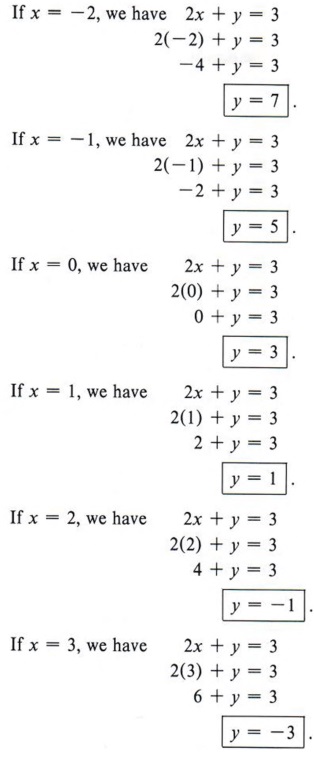 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
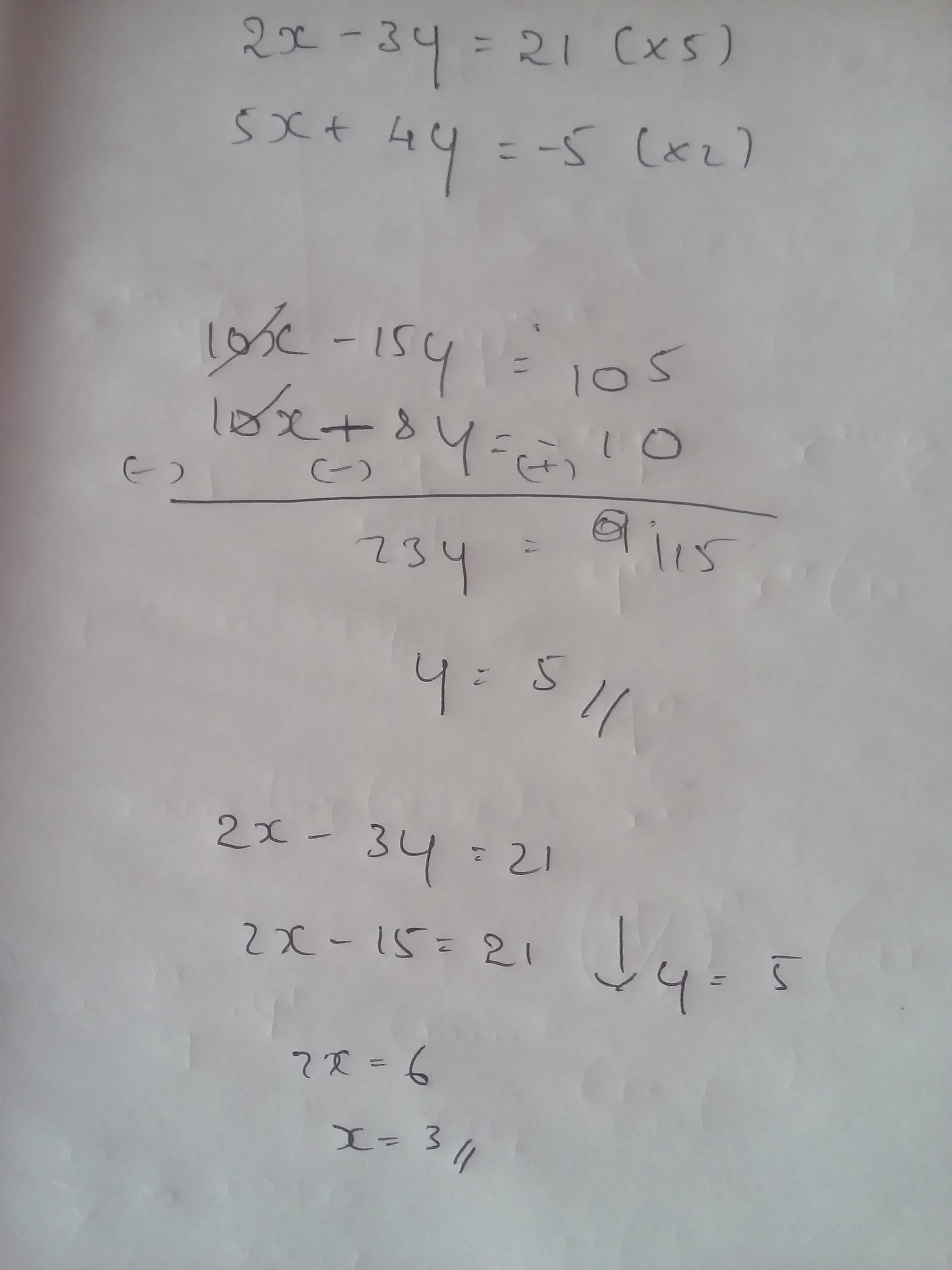 3 X 5 Y 2 2 X Y 4 3y Brainly In | 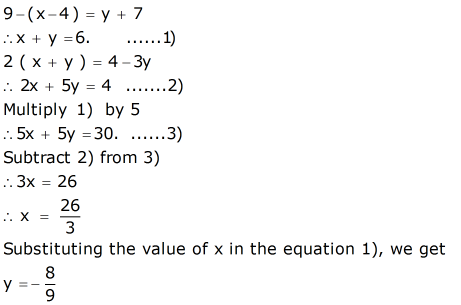 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
 3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In | 3 X 5 Y 2 2 X Y 4 3y Brainly In |
3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |  3 X 5 Y 2 2 X Y 4 3y Brainly In |
「3-(x-5)=y+2 2x+y)=4-3y by elimination method」の画像ギャラリー、詳細は各画像をクリックしてください。
 3 X 5 Y 2 2 X Y 4 3y Brainly In |
Graph 2x3y=5 Solve for Tap for more steps Subtract from both sides of the equation Divide each term by and simplify Tap for more steps Divide each term in by Cancel the common factor of Tap for more steps Cancel the common factor Divide bySolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Incoming Term: 3-(x-5)=y+2 2x+y)=4-3y, 3-(x-5)=y+2 2x+y)=4-3y by elimination method,




0 件のコメント:
コメントを投稿